離散フーリエ変換の行列表現(N=4)
- 積分よりこっちがイメージしやすい人が居るかもしれない
- ここではの場合を示す
- 行列の形には規則性があるので簡単には大きくできる
逆離散フーリエ変換
- フーリエ変換の重要な性質として、逆変換が存在することがある
- 離散フーリエ変換でも逆変換がありInverseでIDFTという
- 定数倍と指数の符号くらいしか変わらない
- ちなみに順と逆のどちらを倍してもいいし符号も逆にしていい
- 両方にを掛ける流儀もある
- 実際にもとに戻ることは自分で確かめるか適当な本を参照してほしい
- 行列表現にして実際に掛けてみるのが簡単かも?
畳み込み定理
- フーリエ変換の重要な性質として畳み込み定理がある
- 畳み込みはConvolutionなのでCNNのCと一緒
- これはフーリエ変換をした結果(周波数成分)の要素ごとの積をとったものの逆変換が入力の畳み込みになっているという定理
- 離散フーリエ変換での畳み込み定理がを法とする多項式乗算になる
- つまり、が以下と同値になる
- まずはこれを証明する
補題:指数が非ゼロなら回転因子の総和がゼロになること
- 前の式が同値なことを示すには以下の式が成り立つことを示す必要がある
- 実際に計算するとたしかにそうなることが簡単にわかる
- なら回転因子が全部打ち消し合う
- 実際に計算するとたしかにそうなることが簡単にわかる
- すべての係数が1の多項式の離散フーリエ変換はで他が0
- 定数関数のフーリエ変換はインパルス関数である
畳み込み定理(続き)
- 補題を利用してさっきの式を展開してみよう
- を法とするので上の項が下の項に足し算として回り込んでくる
- このような回り込み方を正巡回という
- 全係数が1の場合だと簡単に確かめられる
- TFHEではが法なので逆の負巡回が欲しく、工夫がいる
離散荷重変換
- 負巡回を作るにはこれがいる
- Discrete Weighted fourier TransformでDWTともいう
- 離散ウェーブレット変換とは関係ない
- 定義的には下の式のように重みをかけて(逆)離散フーリエ変換をするだけ
- 倍して離散フーリエ変換して逆フーリエ変換すると倍された係数が戻ってくるので割ればもとに戻る
- 重みをうまく選べば負巡回乗算が実現できる
負巡回乗算
- と選んで畳み込み乗算
- さらに上位桁分を虚数部に入れておく
- 虚数部も使うとメモリと計算量の両方を節約できる
- 実数部と虚数部を連続した別の配列にすると変換が簡単
- 1行目から2行目はDFTによる正巡回の乗算として変形する
高速フーリエ変換
- ここまで見たように離散フーリエ変換ができると負巡回乗算ができる
- ∴離散フーリエ変換が高速化できれば負巡回乗算が高速化できる
- そのアルゴリズムが高速フーリエ変換(FFT: Fast Fourier Transform)
2基底周波数間引き高速フーリエ変換(数式)
- 高速フーリエ変換の基本的アイデアは問題の再帰的分割
- 個に分割すると基底
- 以下のような式から2つに分割できることがわかる
2基底周波数間引き高速フーリエ変換(バタフライ図)
- FFTのアルゴリズムを図示したものがバタフライ図
- の添字がぐちゃぐちゃになる(ビットリバース)のは今示しているのがCooley-Tukey型と呼ばれるin-placeなアルゴリズムであるため
- 普通は添字を戻す並び替えかout-placeなStockham型を使う
- 今回は畳み込み乗算さえできればいいので並び替えをする必要がない
- 論文実装のFFTが自前な理由の一つは並び替えがいらないのを利用するため
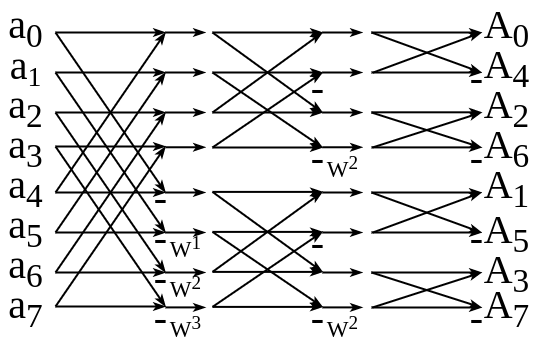
- 論文実装のFFTが自前な理由の一つは並び替えがいらないのを利用するため
2基底周波数間引き高速フーリエ変換(疑似コード)
- in-placeなので受け取った配列を書き換えながら実行される
- 簡潔なので再帰で書いているが最適化しづらいのでForで書くことが多い
Radix2FFT(𝐚,start,end) //startとendは最初0とN
N = start-end
n = (start-end)/2
for x from 0 to n-1
temp = aₓ+aₓ₊ₙ
aₓ₊ₙ = (aₓ-aₓ₊ₙ)*exp(-i2πx/N)
aₓ = temp
if(N>2)
Radix2FFT(𝐚,start,start+n)
Radix2FFT(𝐚,start+n,end)
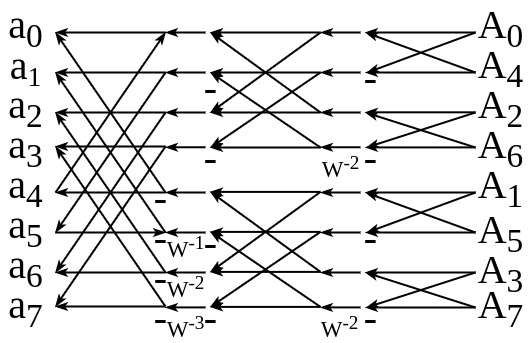
2基底時間間引き高速フーリエ変換
- 周波数間引きの逆変換を時間間引きという
- ビットリバースの並びを入力とする
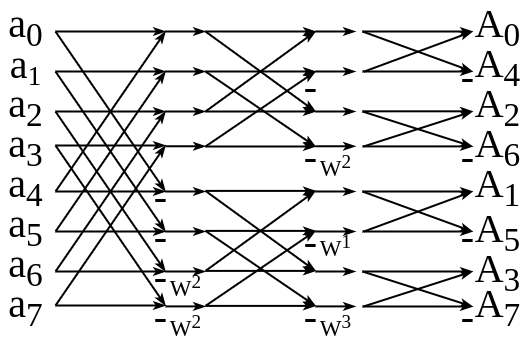
4基底周波数間引き高速フーリエ変換(バタフライ図)
- 左のバタフライ図をぐっと睨むと回転因子を移動させて右のように分解できることがわかる
- なのでこれは乗算にならない

4基底周波数間引き高速フーリエ変換(疑似コード)
Radix4FFT(𝐚,start,end)
N = start-end
if(N==2)
s = start //下付きにするため
temp = aₛ+aₛ₊₁
aₛ₊₁ = aₛ - aₛ₊₁
aₛ = temp
else
n = (start-end)/4
for x from 0 to n-1
for j from 0 to 1
l = j*n
m = l+2*n
temp = aₓ₊ₗ+aₓ₊ₘ
aₓ₊ₘ = (aₓ₊ₗ-aₓ₊ₘ)*i //実数部と虚数部の交換と符号反転
aₓ₊ₗ = temp
for j from 0 to 1
l = j*2*n
m = l+n
if(j==0)
temp = aₓ₊ₗ+aₓ₊ₘ
aₓ₊ₘ = (aₓ₊ₗ-aₓ₊ₘ)*exp(-i2π2x/N)
else
temp = (aₓ₊ₗ+aₓ₊ₘ)*exp(-i2πx/N)
aₓ₊ₘ = (aₓ₊ₗ-aₓ₊ₘ)*exp(-i2π3x/N)
aₓ₊ₗ = temp
Radix4FFT(𝐚,start,start+n)
Radix4FFT(𝐚,start+n,start+2n)
Radix4FFT(𝐚,start+2n,start+3n)
Radix4FFT(𝐚,start+3n,end)
Split Radix(蛇足)
- 4基底で計算量削減効果があるのは下半分だけ
- 上半分は2基底でやめるとSplit-Radixになる
- メモリアクセスやプログラムの煩雑さの都合でSplit-Radixはあまりやらない
- 8基底でも同じことはできる
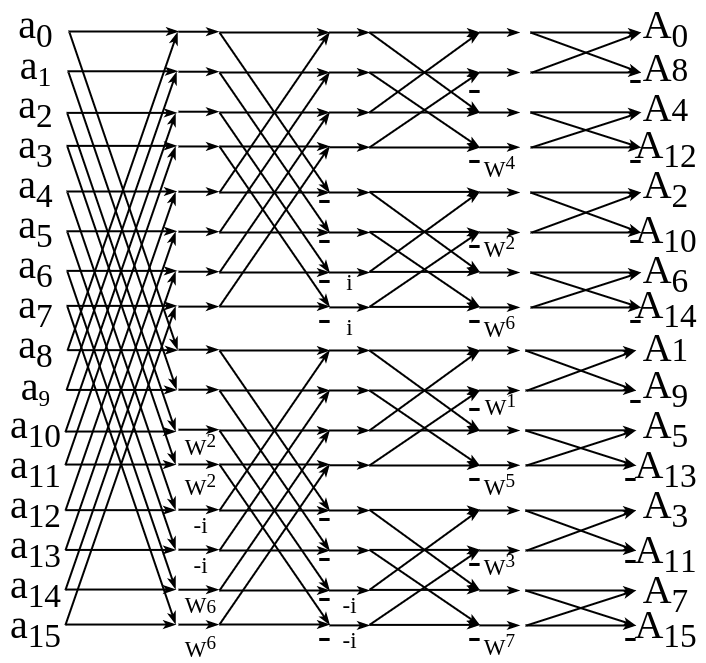
8基底周波数間引き高速フーリエ変換(バタフライ図)
- N=16なのでで乗算が減る
16基底以上のFFT
- 16基底以上も同じように回転因子をまとめていくことで構成できる
- しかし、16基底以上では8基底までで見られたような乗算の削減はできない
- 計算量としては基底が大きいほど下がる
- とはいえ基底を大きくするほど並列性が下がる面もあるのでレジスタの本数やメモリアクセス量との兼ね合いが必要
AVX2について
- x86で定義されているベクトル拡張命令の一つ
- 256bit、倍精度4つ分を1サイクルで計算することができる
- コンパイラに任せるとうまく使ってくれないことがあるので、FFTのように並列計算をゴリゴリやる場合にはアセンブラを書いたほうが速いことがある
- 配列の加算程度ならコンパイラに-march=nativeを渡せば勝手に使ってくれる
TFHEでの利用
- FFTを適切に書けば多項式乗算をこれに置き換えたほうが速い
- 32bit固定小数点数を倍精度に変換して計算する
- 倍精度には符号bitがあるので、符号付きとして解釈したほうが良い
- FFTは実数の上で定義されるので多項式乗算をしている間はトーラスをただの実数とみなし乗算後に剰余を取る
- GPUの場合は倍精度が弱いので数論変換(NTT)を使ったほうが良い
TFHEの多項式乗算における精度要求について
- 倍精度は53bitしか精度がない
- External Productでは最大でを個足したものが結果の係数として出てくる
- これを正確に保持するには少なくともbitの精度が必要
- 今回はで問題ない
- どうせ後で32bitにまるめてしまうので実際は多少はみ出ても問題ない
実装について
- 暗号の本筋とは関係ないのでTFHEの論文実装で使われているSPQLIOSを使うのが良いようには思う
- 有名所のFFT実装としてはIntel IPPやFFTWがあるがこれらは一般的なFFT用途を想定しているためにTFHEで用いるとSPQLIOSに勝てない
- GPUでFFTをするcuFFTもあるがGPUならcuFHEのようにNTTを実装したほうが速い
- SVE2やHIPでの実装はあり?
- AVX512に関しては[]
- NTTに関してはIntel HEXLがある
参考文献
- 円周率.jpの該当ページ(定義を忘れたときとか)
- 大浦先生のページ(FFT実装をするなら必見)
- やる夫で学ぶディジタル信号処理(フーリエ変換一般)
- 道具としてのフーリエ解析(FFT実装をするなら良書)
- 多数桁計算における高速アルゴリズムの研究(一般化されてる)
- The Fastest Fourier Transform in the South
- TFHEのFFT(アセンブラ)
- 講師が書いた8基底FFT(遅い)