TFHE実装入門

4.Blind Rotate

松岡　航太郎

説明内容のHomNANDでの位置づけ

Blind Rotateとは

  • 多項式(TRLWE)を"回転"させる準同型演算
    • "回転"とは要はXXのべき乗をかけるということ
    • べき乗の指数はTLWElvl0によって決まる
  • 入力としてTRLWEとTLWElvl0を1つずつの他にnn個のTRGSWをとる
    • 入力となるTRLWEは特別にTest Vectorと呼ぶ
    • このnn個のTRGSWはlvl0の秘密鍵を1bitずつ暗号化したものでBootstrapping Keyと呼ぶ
  • Test Vectorをうまく選ぶことでTLWElvl0からTRLWEへの関数を作れる
    • Sample Extract Indexも合わせればTLWElvl0からTLWElvl1への関数が作れる
    • ∵Blind RotateによってTLWElvl0の値に応じてTRLWEの係数の位置と符号が変化するので、Sample Extract Indexで取り出す値が変わる

TLWEの丸め

  • べき乗の指数は整数でないと困るのでTLWEを丸める必要がある
    • 指数として意味がある範囲は[0,2N)[0,2N)
      • ∵X2N⋅a[X]≡a[X]mod  XN+1X^{2N}⋅a[X]≡a[X] \mod{X^{N}+1}
    • ∴TLWEを2N2N倍して各係数を[0,2N)[0,2N)に丸めると意味のある数値がとれそう
  • X2NX^{2N}で元に戻るので、丸めた値は2N2Nを法とする剰余環上の値とみなせる
  • ⌊2N⋅(b−a⋅s)⌋mod  2N⌊2N⋅(b-\mathbf{a}⋅\mathbf{s})⌋\mod{2N}を使いたいが秘密鍵は漏らせない
    • 床関数なのは、00に丸まる値を[0,1/2N)[0,1/2N)にするため
    • ⌊2N⋅(b−a⋅s)⌋mod  2N≈⌊2N⋅b⌋−∑i=0n−1⌈2N⋅ai⌋⋅simod  2N=ρ⌊2N⋅(b-\mathbf{a}⋅\mathbf{s})⌋\mod{2N}≈⌊2N⋅b⌋-∑_{i=0}^{n-1}⌈2N⋅a_i⌋⋅s_i \mod{2N}=ρ
    • ⌈2N⋅ai⌋⌈2N⋅a_i⌋は計算可能なのでsis_iとの積が計算できればρρは計算可能/
      図はN=4N=4の場合の例

Blind Rotateのアイデア

  • 実現したい演算は与えられたTRLWEをX−ρX^{-\rho}倍すること
    • 負符号がついているのはその方が綺麗というだけ
  • 秘密鍵を教えずに⌈2N⋅ai⌋⋅si⌈2N⋅a_i⌋⋅s_iを計算したい
    • TRGSWに秘密鍵を暗号化し(Bootstrapping Key)CMUXで各bitが1か0かを反映

Blind Rotateの具体的アルゴリズム

  • N=2NbitN=2^{Nbit}とする(この講義のパラメータではNbit=10Nbit=10)
BlindRotaete((𝐚,b),𝐁𝐊,(𝐚[X],b[X]))
  b̃= b >> (32-Nbit-1)) //ここはfloor
  trlwe = X⁻ᵇ̃⋅(𝐚[X],b[X])
  for i from 0 to n-1
    ã=(aᵢ + (1<<(31-Nbit-1)) ) >> (32-Nbit-1) //足し算は四捨五入をするため
    trlwe = CMUX(𝐁𝐊ᵢ,Xᵃ̃⋅trlwe,trlwe)//Dec(𝐁𝐊ᵢ)?Xᵃ̃⋅trlwe:trlwe
  return trlwe

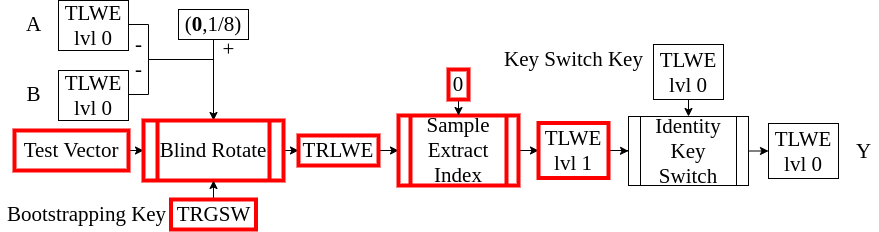
GateBootstrapping TLWE to TLWE(概略)

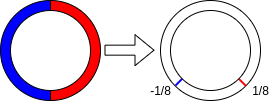
  • 平分の全ての係数が1/81/8であるようなTRLWEを入力としたBlind Rotateを行い、その出力の定数項をSample Extract Indexで取り出す操作の名前
    • ρ∈[0,N)ρ∈[0,N)のとき1/81/8、[N,2N)[N,2N)のとき−1/8-1/8が定数項に来る
    • これはある種の符号関数(暗号文の復号そのもの)
  • 出力となるTLWElvl1のノイズはTLWElvl0のノイズにかかわらず一定になる
    • ∵TLWElvl1のノイズはnn回のCMUXによるノイズのみで固定(Bootstrapping)
    • あとはTLWElvl1からTLWElvl0に変換しないといけないが、その方法は次回

自明な暗号文

  • [0,N)[0,N)で1/81/8を、[N,2N)[N,2N)で−1/8-1/8を取り出せるようなTRLWE(Test Vector)は平文の係数が全て1/81/8であるような暗号文
    • これを普通に暗号化して送ると平文がわかっている暗号文を送ってしまうことになるし、無駄にノイズも増える
  • 実はb[X]b[X]を平文のTorus係数多項式そのままとしa[X]\mathbf{a}[X]を0\mathbf{0}としても有効な暗号文
    • 秘密鍵も乱数生成器もなしで生成できる暗号文なので自明な暗号文と呼ぶ
    • もちろん情報を守ることはできないので使いどころは限られる

GateBootstrapping TLWE to TLWE(疑似コード)

GateBootstrappingTLWEtoTLWE((𝐚,b),𝐁𝐊)
  testvec = (0,0)
  for i from 0 to N-1
    testvec += (0,μXⁱ)
  trlwe = BlindRotate((𝐚,b),𝐁𝐊,testvec)
  return SampleExtractIndex(trlwe,0)

なぜlvl0とlvl1が必要なのか

  • 原理的にはlvl1だけで構成することは可能
  • nnはBlindRotateでのCMUXの個数なのでこれを減らしたい
  • BlindRotateではTorusを[0,2N)[0,2N)に丸める
    • この丸め誤差がn+1n+1個入るがこれは一般に暗号文のノイズに比して大きい
    • Bootstrappingの誤り確率を抑えるためにnnを小さくしたい

Blind Rotateで最低限実装するべきもの

  • GateBootstrapping TLWE to TLWE
    • 任意のTRLWEをとるBlind Rotateを実装する必要はない
      • とはいえ特殊化しても知る限り性能メリットはない

page_number: true