完全準同型暗号入門

佐藤研究室 松岡　航太郎
gmail: matsuoka.kotaro

準同型暗号とは？

  • 「暗号文のママ計算できる」暗号
  • 平文に対する演算と準同型な演算を暗号上で定義できる
  • 概念が提案されたのは1978年(RSAと同年)
  • DARPA、Intel、IBM、Microsftなどが鎬を削っている
  • 流行りの応用は医療データなどの機密性の高いデータを扱うPrivate AI

準同型暗号の例: RSA暗号

  • p,q∈P,n=pq,e≤ϕ(n)=(p−1)(q−1),d=e⁻¹ mod np,q∈ℙ,n=pq,e≤ϕ(n)=(p-1)(q-1),d=e⁻¹ \bmod nとする
  • c,mc,mを暗号文と平文を示すものとする
  • 暗号化: c≡mᵉ mod nc ≡ mᵉ \bmod n, 復号 mᵈ mod nmᵈ \bmod n'
  • 実はこれが乗算について準同型暗号になっていることを見よう
  • すなわち、２つの暗号文を掛け算して復号すると平文の掛け算が得られる
  • (c1⋅c2)d=(m1e⋅m2e)d=(m1⋅m2)ed≡m1⋅m2 mod n(c_1 ⋅ c_2)^d = (m_1^e ⋅ m_2^e)^d = (m_1⋅m_2)^{ed} ≡ m_1⋅m_2 \bmod n

準同型暗号の種類

今日では以下の4つに分けられる
基本的に上に行くほど制限が強く、下に行くほど計算が重い

  • 部分(Partially)準同型暗号 (PHE): 加算か乗算だけをサポートするもの
    • ex. RSA暗号、ElGamal暗号、Paillier暗号など
  • Somewhat HE: 両方できるが演算回数に暗号形式に依存した制限が在るもの
    • 格子ベースでないものは知る限りではここが限界
    • ex. Xbyak作ってる光成さんのやつ
  • Leveled HE: 演算回数の制限がパラメータで変更できるもの
    • 暗号上で評価する関数の空間を暗号化時に制限する必要が在る
  • 完全(Fully)準同型暗号: 任意の関数が評価できる
    • 今日の本題なので詳しくは後述

Learning With Error (LWE)

  • 最もよく知られている格子暗号でNP困難なShort Vector Problemに依拠する(提案はRegevさんの2005年)
  • これの拡張が耐量子暗号の候補としてNIST Round3まで生き残っている
  • ここでは全係数が剰余環上にとられるInteger LWEを紹介する
  • n,q∈Z+n,q∈ℤ^+を公開パラメータ、s∈Zn,a∈Zqn\mathbf{s}∈ℤ^n,\mathbf{a}∈ℤ_q^nは各係数が一様分布、e∈Zqe∈ℤ_qは正規分布に従って取られるものとする
  • s\mathbf{s}は秘密鍵で、eeはエラー(またはノイズ)
  • Zq∋b=a⋅s+m+eℤ_q∋b=\mathbf{a}⋅\mathbf{s}+m+eとして、(a,b)(\mathbf{a},b)の組が暗号文
  • 復号はb−a⋅s=m+eb-\mathbf{a}⋅\mathbf{s}=m+eから一番近いあり得る平文に丸める

LWEの加法準同型性

  • 実はLWEはそのままでも加法が定義できることを確認する
  • (a1,b1)+(a2,b2)=(a1+a2,b1+b2)(\mathbf{a}_1,b_1)+(\mathbf{a}_2,b_2)=(\mathbf{a}_1+\mathbf{a}_2,b_1+b_2)とする

(b1+b2)−(a1+a2)⋅s=(b1−a1⋅s)+(b2−a2⋅s)=m1+m2+e1+e2\begin{aligned}(b_1+b_2)-(\mathbf{a}_1+\mathbf{a}_2)⋅\mathbf{s}&=(b_1-\mathbf{a}_1⋅\mathbf{s})+(b_2-\mathbf{a}_2⋅\mathbf{s})\\&=m_1+m_2+e_1+e_2\end{aligned}

  • ここで重要なのは加法によってエラーeeも増えること
  • エラーが増えすぎると復号で誤ったメッセージに丸める可能性が在る
  • ∴任意の関数を評価するにはエラーを除去する必要が在る

Bootstrapping

  • 準同型暗号上で復号関数を評価することでエラーを除去する操作のこと
  • Gentryさんはこれを最初に提案し、構成を与えた
  • 現状の完全準同型暗号は全てこれによって構成されている
  • あとでTFHEにおけるBootstrappingのアイデアを見る

完全準同型暗号

以下の4つの世代に分けられる

  • 第１世代: SHEを使ってBootstrappingを構成したもの
    • 効率の問題などで現実に用いられることはほぼない
  • 第２世代: 剰余環上の乗算と加算をサポートするもの
    • 第２世代を構成する過程でLHEが作られ、以降はそれをベースとしている
    • ex. BGV(Brakerski-Gentry-Vaikuntanathan),BFV(Brakerski/Fan-Vercauteren)
  • 第３世代: バイナリ演算をサポートするもの
    • Bootstrappingが他の世代に比して高速(1000倍のオーダ)
    • ex. GSW(Gentry-Sahai-Waters),TFHE(Torus FHE)
  • 第４世代: 有限精度複素数演算をサポートするもの
    • 実数が扱えるので深層学習用途に人気
    • ex. CKKS(Cheon-Kim-Kim-Song)

TFHE

  • 第３世代FHEの一つ
  • 知られている中で最も高速なBootstrapping(10msオーダ)
  • バイナリ演算以外の非線形演算の評価にも適している(ReLUなど)
  • VSPではプロセッサ回路の評価に使用

Torus

  • 円周群のこと(複素数平面の単位円上の点がなす群)
  • ここではR mod 1\mathbb{R} \bmod 1を定義とする。つまり、実数の小数部分で、[0,1)[0,1)または[−0.5,0.5)[-0.5,0.5)に値をとる
  • Torusの集合を𝕋𝕋と書く
  • 加算の例: 0.8+0.6=1.4≡0.4 mod 1,0.3−0.9=−0.6≡0.4 mod 10.8+0.6=1.4≡0.4 \bmod 1,0.3-0.9=-0.6 ≡ 0.4 \bmod 1
  • 乗算は定義できない。1.2≡0.2 mod 1,2.4≡0.4 mod 11.2≡0.2 \bmod 1,2.4≡0.4 \bmod 1なので、乗算が定義できるなら1.2⋅2.4=2.88≡0.2⋅0.4=0.08 mod 11.2⋅ 2.4=2.88≡0.2⋅0.4=0.08\bmod 1だが成立しない。
  • 整数(Z\mathbb{Z})との乗算は定義できる例3⋅0.4≡0.2 mod 13⋅ 0.4≡ 0.2 \bmod 1
  • 実装レベルでは、32bitないし64bit整数を固定小数点数として使う

TLWE

  • Torus版のLWE
  • 全ての係数がTorusのもの(つまり平文もエラーもTorus)
  • 秘密鍵はZnℤ^nなのでa⋅s\mathbf{a}⋅\mathbf{s}は問題なく計算できる
  • 実際にはTFHEでは高速化のためにs∈𝔹n\mathbf{s}∈𝔹^nにとる
  • 実装としてはq=232q=2^{32}などにとったInteger LWEと同じになる
  • qqの選択を忘れられるので理論として綺麗になる

TFHEにおけるメッセージエンコードの仕方

  • 復号で丸めをするのでメッセージ空間を制限する必要が在る
  • TFHEでは0と1を表現させたい(mb∈𝔹m_b∈𝔹とする)
  • これをTorusの平文としてm=(2mb−1)/8∈𝕋m=(2m_b-1)/8∈𝕋にエンコードする
  • 8で割る理由は次スライド
  • 復号は(1+sgn(b−a⋅s))/2(1+\mathit{sgn}(b-\mathbf{a}\cdot\mathbf{s}))/2
  • 符号関数sgn\mathit{sgn}が丸めになっている

バイナリ演算のアイデア

  • Torusにエンコードされた平文は{-1/8,1/8}
  • ２つのTLWEを足したものの平文は{-1/4,0,1/4}
  • これに(0,−1/8)(\mathbf{0},-1/8)を足すと{-3/8,-1/8,1/8}
  • -3/8になるのは両方の暗号文がバイナリの平文として0のとき
  • 1/8は両方1、-1/8は２つが異なる
  • この暗号文を復号すると、負符号のものは0に、正符号は1になる
  • つまり、両方1の暗号文を入力としたときだけ1になるのでANDになっている
  • Remark: Bootstrappingは暗号上で復号を評価する

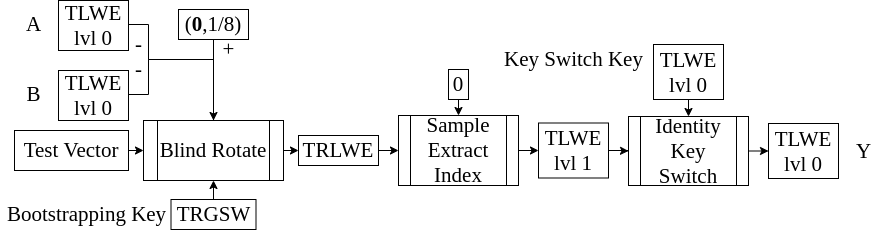
HomNAND

  • Bootstrappingを使ってNANDを評価する方法
  • 任意の２入力ゲートは足し算の符号と定数を変えることで構成可能
  • TFHEで実際に復号を評価するためのアイデアを見ていく

width:1200px

TRLWE

  • Ring版のTLWE
  • ここで言うRingは多項式環のこと
  • TFHEではN∈Z+N∈ℤ^+を公開パラメータとしてXN+1X^N+1で割った余りを考える
  • 原則的にはNNは2のべき乗である(円分多項式は有理数の範囲で既約)
  • Torus係数多項式をXN+1X^N+1で割った余りの成す環を𝕋N[X]𝕋_N[X]と書く
  • 平文とエラーはm[X],e[X]∈𝕋N[X]m[X],e[X]∈𝕋_N[X]となり、秘密鍵もs[X]∈ZN[X]s[X]∈ℤ_N[X]となる
  • 暗号文はb[X]=a[X]⋅s[X]+m[X]+e[X]b[X]=a[X]⋅s[X]+m[X]+e[X]として(a[X],b[X])(a[X],b[X])
  • 復号はb[X]−a[X]⋅s[X]b[X]-a[X]⋅s[X]を各係数ごとに丸める

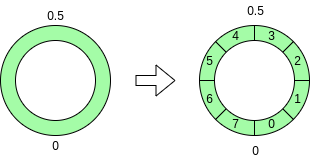
Blind Rotateとは

  • 多項式をTLWEに対応した度合いだけ「回転」させる操作
  • ここでいう「回転」は要はXのべき乗をかけるということ
  • 回転させた後に定数項を取り出す(Sample Extract Index)
  • Xの指数を入力に依って決めることで回転の度合いを変える
  • 重要な事実は、𝕋N[X]∋p[X]=∑i=0N−1piXi𝕋_N[X]∋p[X]=∑_{i=0}^{N-1}p_iX^iとすると
    X⋅p[X]≡−pN−1+∑i=0N−2piXi+1 mod XN+1X⋅p[X]≡-p_{N-1}+∑_{i=0}^{N-2}p_iX^{i+1} \bmod X^N+1(負巡回)
    XN⋅p[X]≡−p[X] mod XN+1,X2N⋅p[X]≡p[X] mod XN+1X^{N}⋅p[X]≡-p[X] \bmod X^N+1,X^{2N}⋅p[X]≡p[X] \bmod X^N+1
    Xf⋅Xg⋅p[X]≡Xf+g mod 2N⋅p[X] mod XN+1X^f⋅X^g⋅p[X] ≡ X^{f+g \bmod 2N}⋅p[X] \bmod X^N+1
  • つまり、N個の係数とその符号反転で最大2N個のユニークな数値を取り出せる
  • これは1種のLook Up Table(LUT)とみなせる
  • Blind Rotateは、この操作を入力となるTLWEのエラーに結果のエラーが依らないようにできる

Blind Rotateのアイデア

  • 入力となるTLWEを(a,b)(\mathbf{a},b)、[−N,N)∋ρ=⌈2N⋅b⌋−∑i=0N−1⌈2N⋅ai⌋ mod 2N[-N,N)∋ρ=⌈2N⋅b⌋ - ∑_{i=0}^{N-1}⌈2N⋅a_i⌋ \bmod 2Nとする
  • ρρの計算はTorus上での丸めの準同型演算であるとも見れる
  • 今評価したいのは復号の要である符号関数
  • 全ての係数が1/81/8である多項式をt[X]∈𝕋N[X]t[X]∈𝕋_N[X]とする
  • X−ρ⋅t[X]X^{-ρ}⋅t[X]の定数項の符号はρρ(≈b−a⋅s≈b-\mathbf{a}⋅\mathbf{s})の符号と同じになる
  • ∵ 0≤ρ<N⇒0≤ρ<N⇒定数項はtρ=1/8,−N≤ρ<0⇒−tN+ρ=−1/8t_ρ=1/8,-N≤ρ<0⇒-t_{N+ρ}=-1/8
  • Remark: 入力のエラーは隣のスロットを選ぶ可能性をもたらすが、ρρの符号が変わらないなら結果に影響を及ぼさない
    w:300px

TRGSW

  • Torus版Ring版 GSW(最初の第3世代FHE)
  • この暗号文形式が在るのがTFHEが第３世代である所以とも言える
  • 説明しだすと長いので詳細は省略
  • 平文がμ[X]∈Z[X]μ[X]∈ℤ[X]に取られることと、以下の演算が定義されることだけが大事
  • 実際にはμ[X]μ[X]は𝔹𝔹にとられる(理由は次のスライド)

External Product

TRGSW⊡TRLWE→TRLWE

  • 平文の計算としてはμ[X]⋅m[X]μ[X]⋅m[X]

CMUX

  • C\mathbf{C}を平文が𝔹𝔹なTRGSW、c1[X],c0[X]c_1[X],c_0[X]をTRLWEとする
  • 以下の計算はC\mathbf{C}の平文が1ならc1[X]c_1[X]を、0ならc0[X]c_0[X]を返す
    C⊡(c1[X]−c0[X])+c0[X]\mathbf{C}⊡(c_1[X]-c_0[X])+c_0[X]
  • これを使いたいので平文は𝔹𝔹だけでよい

CMUXを使ったBlind Rotateの構成

  • Remark: TRLWEのa[X],b[X]a[X],b[X]をそれぞれX倍すると平文もX倍される
  • 前に述べたように、s∈𝔹n\mathbf{s}∈𝔹^nにTFHEは制限している
  • BKi\mathbf{BK}_iをs\mathbf{s}のii番目の係数を平文とするTRGSWとする
  • X−ρ⋅t[X]X^{-ρ}⋅t[X]は以下のような疑似コードで暗号上で計算することができる
  • Remark: 出力のエラーは入力のTLWEのエラーに依存しない
BlindRotaete((𝐚,b),𝐁𝐊)
  b̃=2N-⌈2N⋅b⌋
  trlwe = (0,X⁻ᵇ̃⋅t[X])
  for i from 0 to n-1
    ã=⌈2N⋅aᵢ⌋
    trlwe = CMUX(𝐁𝐊ᵢ,Xᵃ̃⋅trlwe,trlwe)//Dec(𝐁𝐊ᵢ)?Xᵃ̃⋅trlwe:trlwe
  return trlwe

Sample Extract Index

  • 任意の次数の係数をTRLWEから取り出してTLWEを構成する操作
  • b[X]−a[X]⋅s[X]b[X]-a[X]⋅s[X]のkk次の係数は以下のように書ける
    bk−(∑i+j=k,0≤i,j≤N−1ai⋅sj)−(∑i+j=N+k,0≤i,j≤N−1−ai⋅sj)b_k-(∑_{i+j=k,0≤i,j≤N-1}a_i⋅s_j)-(∑_{i+j=N+k,0≤i,j≤N-1}-a_i⋅s_j)
  • s′\mathbf{s}'はs[X]s[X]のii次の係数をii番目の要素とするベクトル
  • 00次の係数を取り出したTLWEを(a′,b0)(\mathbf{a}',b_0)とするとa′\mathbf{a}'はa0′=a0,ai′=−aN−ia_0'=a_0,a_i'=-a_{N-i}
  • これはb0−a′⋅s′b_0-\mathbf{a}'⋅\mathbf{s}'が上の式でk=0k=0とした場合と同じになっている
  • このTLWEはa′\mathbf{a}'の次数がnn(lvl0)ではなくNN(lvl1)になっている
  • これを変換するのがIdentity Key Switch

Identity Key Switch

  • Key SwitchはTLWEを異なる秘密鍵のTLWEへと変換する操作(s′→s\mathbf{s}'→\mathbf{s})
  • 基本的なアイデアはb′−∑i=0N−12−t⌈2t⋅ai′⋅si′⌋b'-∑_{i=0}^{N-1}2^{-t}⌈2^t⋅a_i'⋅s_i'⌋を暗号上で計算すること
  • KSᵢⱼをs\mathbf{s}を秘密鍵、2−j⋅si′2^{-j}⋅s'_iを平文とするTLWEとする
IdentityKeySwitch((𝐚',b'),𝐊𝐒)
  b̃=b'
  for i from 0 to n
    ãᵢ = 0
  for i from 0 to N
    for j from 0 to t-1
      (𝐚̃,b̃) -= (⌊aᵢ'*2ʲ⁺¹⌋ mod 2) ⋅ KSᵢⱼ
  return (𝐚̃,b̃)

HomNAND(再掲)

  • これらを全てつなげるとNANDが評価できる
  • 説明しなかったのはTRGSWの話だけ(一番面倒では在る)

width:1200px

準同型暗号の展望

  • TFHEのゲートは10msかかるので物理論理ゲートに比べると10⁹ほど遅い
  • 他の準同型暗号も平文の演算に比べるとずっと遅い
  • DARPAはこれを専用ハードウェアで押し切ろうとしている
  • そもそもまだ暗号学的改善の余地も在る
  • 標準化の動きも在る
  • 謎の準同型暗号ベンチャーは雨後の筍状態
  • 理論的な問題としてはMalleabilityの問題が在る
  • 準同型暗号は秘密計算の「聖杯」≠「銀の弾丸」

page_number: true