Introduction to TFHE Implementation

1.TLWE

Kotaro Matsuoka

Position of Explained Content in HomNAND

• lvl1 will be explained next time, so for now TLWE means lvl0

What is TLWE

• Stands for Torus Learning With Errors
• Means LWE encryption using Torus
• LWE is explained in the next slide

What is LWE

• Integer LWE, which takes values in quotient rings, is commonly used
  • Its extension was selected for NIST PQC as post-quantum cryptography
• As the name suggests, Error plays an important role
  • When you can obtain as many ciphertexts with known plaintext as you like (IND-CPA), if there is no Error, you can find the secret key by calculating the inverse of the matrix obtained by arranging of the obtained ciphertexts
    • With Error, it deviates from a simple inverse matrix problem, and the larger the Error, the harder it becomes
    • With real numbers it would be least squares, but it's harder because some discretization is involved
• The larger the matrix size (), the harder it is

Intuitive Definition of Torus

• Also known as circle group, written as .
• It's good to imagine the angle of a clock hand
• As a concrete number, it's the angle of the hand divided by 2π

What is Torus

• Here, we define it as . That is, the fractional part of a real number, taking values in or
  • For understanding the theory, alone is sufficient
  • may be more efficient in implementation
• Multiplication between Torus values is not defined, but addition is
• Example of addition: ,
• Multiplication cannot be defined. Example: Since and , if multiplication could be defined, , but this doesn't hold
• Multiplication with integers () can be defined. Example:

Modular Gaussian Distribution

• Used in the original TFHE paper
• Normal distribution samples take values in real numbers (), but this takes values in Torus
  • Discrete Gaussian distribution is defined on integers, but this is Torus
  • Since actual implementation approximates to integers, there's an argument that discrete Gaussian distribution or CBD should be used
  • Uniform distribuiton is another option, since we can define it naturally in Torus
• Samples from normal distribution taken give modular normal distribution
  • Using this for error is most standard (not best) in TFHE

Specific Construction of TLWE (when plaintext is Torus)

• is the set of binary values.
• Two parameters determine encryption security:
• Let be the uniform distribution taking values independently from
• Let be the modular normal distribution with mean and standard deviation
• Let , , ,
• is plaintext, , ,
• Ciphertext is , an element vector, where
• Since , if we add a method to remove , we can extract and decrypt
• The larger and , the more secure (if is too large, the ciphertext breaks)

Visual Image (Noise from Encryption)

Plaintext	With Noise

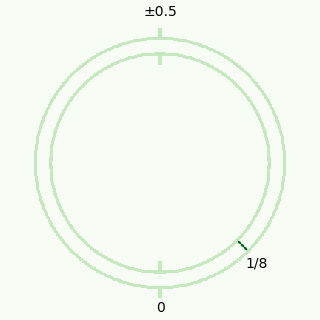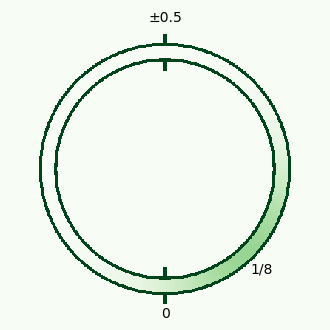• As emphasized, the probability of decryption error is not zero (negligible in practice)
  • Generally, below is considered acceptable
  • It's said that this is about the error probability on a typical PC

Additive Homomorphism of TLWE

• Consider two ciphertexts , , and let their sum be
• , and since appears, we can see additive homomorphism
• Since the error also becomes , there is a limit to the number of additions that can be performed
  • If the error is too large, the probability of decryption error increases

Specific Construction of TLWE (when plaintext is binary)

• Let ,
• TLWE ciphertext is
• Decryption is ( is the sign function)
• During decryption,

Visual Image (Addition without Noise)

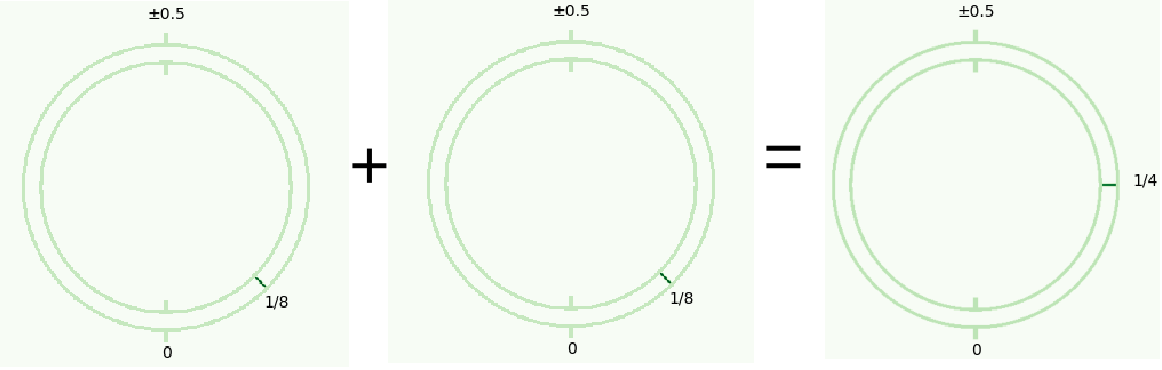
Visual Image (Addition with Noise)

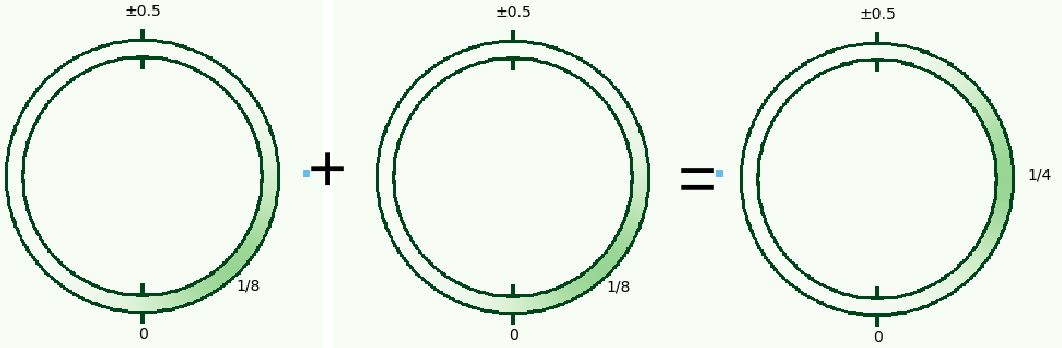
Idea of Binary Operations

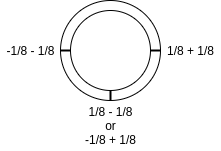
• Plaintext encoded in Torus is {-1/8, 1/8}
• Plaintext of sum of two TLWEs is {-1/4, 0, 1/4}
• Subtracting this from gives {-1/8, 1/8, 3/8}
• -1/8 occurs when both ciphertexts are 1 as binary plaintext
• 3/8 when both are 0, 1/8 when the two are different
• When decrypting this ciphertext, negative signs become 0, positive signs become 1
• That is, it becomes 0 only when both input ciphertexts are 1, so it's NAND
  • ∴ If decryption can be evaluated on ciphertext, NAND can be computed on ciphertext

Visual Image (All Patterns of Addition without Noise)

• When subtracting the sum of two inputs from , only when both are 1 is it in the left half
• Becoming 0 only when both are 1 is exactly NAND
  • The signs and constant values for the initial addition/subtraction are determined this way
  • Other 2-input logic gates can be made by choosing similarly
    

Bootstrapping

• The operation of removing error by evaluating the decryption function on homomorphic encryption
• Craig Gentry first proposed this and gave a construction
  • All current fully homomorphic encryptions are constructed by this
  • In TFHE, the operation called Blind Rotate is essentially Bootstrapping

Implementation of Torus

• Since it's a set of fractional parts of real numbers, one naturally wants to implement it with double-precision floating-point numbers
  • However, with floating-point numbers is heavy
• Therefore, we use fixed-point numbers where the decimal point is before the most significant bit
• Example: For 8-bit width, is , is
• With this method, the integer part from addition or multiplication is discarded by overflow, so modulo operation is not needed
• Example: For 8-bit width,
• The width of the fixed-point number should be sufficient to express
  • That is, the sufficient width is determined by the standard deviation of the modular normal distribution

Implementation of Real Number and Torus Conversion

• Implementation of modular normal distribution requires conversion between real numbers and Torus
• Ideally, it's the operation of extracting the fractional part of a real number
• Let the operation to extract the integer part of a real number be , the fixed-point width be , and the input real number be
• To extract just the fractional part of a real number, is sufficient
• Actually, since we want a fixed-width fixed-point number, we extract the top digits of the real number as an integer
• The operation we want to implement can be written as the following formula

Centered Binomial Distribution (CBD)

• One of the noise distributions used besides modular normal distribution
  • Discrete normal distribution is also commonly used
  • Since it cannot be defined on Torus, it can only be used after discretizing Torus
• Defined using random variables that take 0 or 1 with equal probability

• is a parameter, and as it increases, the tail widens
• Advantages are ease of computation and bounded value range

About TLWE Parameters

• In this lecture, we introduce values currently estimated to be 128-bit security
• , or , fixed-point width is 16 bits
• TLWE security reduces to LWE security problem, so LWE estimation methods can be used
  • Theory is explained with Torus, but implementation uses quotient ring with modulus
    • In that sense, discrete normal distribution or CBD should be used rather than modular normal distribution
  • Which is more essential, quotient ring or Torus? (I sometimes wonder)
• LWE Estimator is the de facto standard for security evaluation
  • Code example for security estimation is here

About Random Number Generation

• Encryption security is greatly affected by random number quality
• Mersenne Twister should not be used (Pokemon RNG manipulation)
  • The original paper author's implementation uses it, but don't imitate
• The safest is to use random numbers provided by the OS (on Linux, /dev/urandom)
• Pseudorandom numbers whose cryptographic security is guaranteed are called CSPRNG (Cryptographically Secure PseudoRandom Number Generator)
  • TFHEpp uses BLAKE3's eXtended Output Function (XOF) mode

Minimum Implementation for TLWE

• Just list what's needed to make HomNAND, so whether to make it more general is up to design philosophy
• Just implement encryption and decryption limited to binary plaintext
• Addition of ciphertexts is used later, so it's good to hold data in a way that makes vector-like addition easy
  • TFHEpp holds it with std::array, but overloading operators with classes is more common
    • Depending on your philosophy
  • The form rather than is more common
    • Recently I feel this is slightly more efficient in terms of memory access
• Parameters should be written so they can be easily changed later for higher versatility